Đánh số 9 đồng xu, từ 1 đến 9
Bỏ đồng thứ 9 riêng ra, chia 8 đồng thành 2 nhóm: A gồm 1 2 3 4 và B gồm 5 6 7 8
Lần cân 1: Cân 2 nhóm A và B với nhau, các trường hợp xẩy ra.
TH1: đĩa cân lệch nhau, giả sử A nhẹ hơn B, Như vậy có các giả thiết
- Trong nhóm A gồm 4 xu 100g; trong nhóm B có 3 đồng 100 và 1 đồng 110 (như vậy đồng số 9 phải là đồng 90g)
- Trong nhóm A có 3 đồng 100g và 1 đồng 90; nhóm B có 4 đồng 100g (như vậy đồng số 9 phải là đồng 110g)
- Trong nhóm A có 3 đồng 100g và 1 đồng 90; nhóm B có 3 đồng 100g; 1 đồng 110g (như vậy đồng số 9 phải là đồng 100g)
Có thể thấy, trong lần cân này, đồng 90g ko bao giờ nằm ở phía nặng cân hơn.
chia lại thành 4 nhóm, mỗi nhóm 2 xu. Nhóm (a: 1 2) (b: 3 4); (c: 5 6); (d:7 8).
Khi đó tiếp tục cân lần 2: cân a c và b d
- Nếu 2 bên bằng nhau, như vậy, đồng 90 nằm ở a, đồng 110 nằm ở c hoặc đồng 90 nằm ở b và 110 nằm ở d. Đồng số 9 sẽ là 100g. Cân lần 3: a và b, bên nào nhẹ hơn thì bên đó có đồng 90, giả sử a nhẹ hơn, như vậy trog 1 và 2 có 1 đồng 90 và 5 và 6 có 1 đồng là 110; cân lần 4: 1 5 và 2 6; nếu bằng nhau thì 1 là 90; 5 là 110; nếu 1 5 nhẹ hơn thì 1 là 90; 6 là 110 => xong
- Nếu cân lệch nhau, thì bên nào nặng hơn sẽ có đồng 110, giả sử ac nặng hơn, như vậy đồng 110 phải nằm trong c. Cân lần 3 a và b, nếu bằng nhau thì đồng 9 là đồng 90, cân lần 4 giữa 5 và 6 đồng nào nặng hơn là 110. Nếu lần cân 3, a và b lệch nhau, bên nào nhẹ hơn sẽ có đồng 90, giả sử là a. Cân lần 4 như trên, 1 5 và 26, tiếp tục suy luận như trên để tìm ra => xong
TH2: sau lần cân 1, Đĩa cân bằng nhau, như vậy chỉ có 1 trường hợp là 1 bên 4 đồng 100g; bên kia 2 đồng 100, 1 đồng 90, 1 đồng 110; đồng số 9 là 100g
chia lại thành 4 nhóm, mỗi nhóm 2 xu. Nhóm (a: 1 2) (b: 3 4); (c: 5 6); (d:7 8)
Lưu ý: 2 đồng xu khác biệt lúc này chỉ có thể hoặc nằm ở nhóm a b hoặc ở c d
Cân lần 2: a c và b d. Các tình huống:
- Cân thăng bằng: trường hợp này cho thấy cả 2 đồng xu khác biệt đã chui vào cùng 1 tổ hợp (a, b, c hoặc d)
Lấy trong tổ hợp a, b, c mỗi tổ hợp 1 đồng xu, giả sử là 1 3 5, lấy thêm đồng xu số 9 là có 4 xu.
Cân lần 3 : 1 3 và 5 9
Nếu bằng nhau, suy ra 2 đồng khác biệt là 2 đồng 7 8, cân 2 đồng này để biết đồng nào 90, 100
Nếu 1 3 và 5 9 chênh lệch, có các tình huống
- 5 9 nhẹ hơn: Tức là: hoặc đồng 5 là đồng 90g (khi đó đồng 6 là 110); hoặc trong 2 đồng 1 3 có 1 đồng là 110 (và 5 là 100); lúc này cân lần 4: 1 9 và 3 5; sẽ ko thể có trường hợp bằng nhau ở đây. Nếu 3 5 nặng hơn, thì tức là đồng 3 là 110, 5 là 100. À khi đó 4 là đồng 90; nếu 3 5 nhẹ hơn thì 5 là đồng 90 và 6 là đồng 110
- 5 9 nặng hơn thì làm tương tự cũng phân biệt được luôn
- Cân ko thăng bằng sau lần cân 2, như vậy 2 đồng xu khác biệt đã được tách ra nằm trong 2 tổ hợp. Ở đây tôi giả sử Giả sử a c nặng hơn (nhẹ hơn thì ở dưới làm ngược lại tương tự nhé), như vậy đồng 110 sẽ hoặc là nằm trong a (khi đó đồng 90 phải nằm trong b); hoặc nằm trong c (khi đó đồng 90 phải nằm trong d).
Cân lần 3: lấy a cân với c, nếu a nặng hơn chứng tỏ đồng 110 nằm trong a và đồng 90 nằm trong b; nếu a nhẹ hơn, chứng tỏ đồng 110 nằm trong c và đồng 90 nằm trong d.
Tôi giả sử là 110 nằm trong a,
Nhiệm vụ là 1 lần cân còn lại tìm ra đồng 110 là đồng nào trong 1 và 2; đồng 90 là đồng nào trong 3 và 4.
Làm như sau:
Cân lần 4: 1 3 và 5 9
Nếu bằng nhau: 1 là 110, 3 là 90
Nếu 1 3 nặng hơn: 1 là 110, 4 là 90
Nếu 1 3 nhẹ hơn: 2 là 110; 3 lag 90
NHIỆM VỤ HOÀN THÀNH !
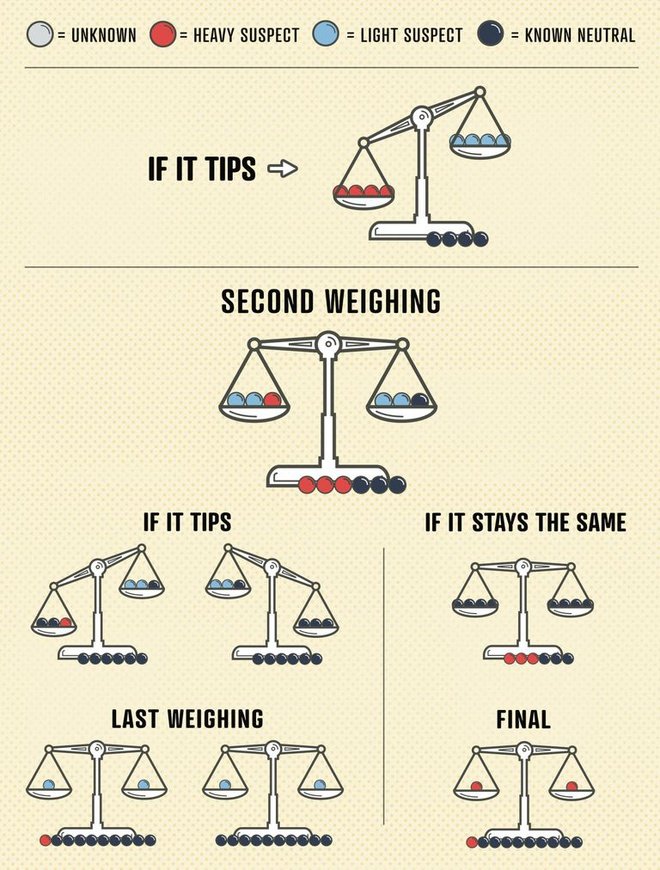
Cụ này nói chuẩn này, lớp 6 chưa học vật lý nên làm cách này không lo bị ăn đòn
