[Funland] Nhờ các cụ thông thái giải giúp bài toán 11

[herotran8]

thế bài cháu giải dùng tổ hợp hay chỉnh hợp cụ?

Bài này dùng tổ hợp là chuẩn rồi. cái này ngày xưa em học giỏi nhất lớp. Lớp 8 thì phải. Cách đây 23 năm rồi.

 

[kienvinh]

Tính như thế này bị lặp lại rất nhiều lần với nhóm 2 bs nam + 1 y tá nữ và 1 bs nam + 2 y tá nữ

Bác nói đúng.

2 Bs nam và 1 y tá nữ chỉ có 5 trường hợp chứ không phải 10, vì không quan tâm đến thứ tự Bs nam (nếu Bs nam xếp đầu làm trưởng đoàn thì lại là 10 trường hợp).

1 Bs nam và 2 y tá nữ: đây thực ra là chọn tổ hợp chập 2 của 5, tức là có bao nhiêu cách chọn 2 phần tử từ tập hợp 5. Được kết quả bao nhiêu nhân 2, vì có 2 Bs nam.

Thế thôi.

 

[bimbim5656]

3 trg hợp:
- 2 bác sỹ, 1 y tá nữ: 2C2.5C1=5.
- 1 bs, 2 y tá nữ: 2C1.5C2=20.
- 1 bs, 1 t tá nam, 1 y tá nữ: 2C1.3C1.5C1=30.
Tổng: 55.

 

[ngày giữa đêm]

Chia 5 đôi xoạc vừa đẹp
Em fun chút , nhưng bài toán hình như thiếu dữ kiện .

Đáp án: Bổ nhiệm em làm trạm trưởng

 

[Đá Ốp Lát]

+ Hoặc chọn 1BS nam + 1 ytá nữ + 1 ytá nam : có 2x5x3 = 30 cách
+ Hoặc chọn 1BS nam + 2 ytá nữ : có 2x5x4 = 40 cách
+ Hoặc chọn 2BS nam + 1 ytá nữ : có 1x5 = 5 cách

Tổng: 30 + 40 + 5 = 75.

F1 nhà em học lớp 11, hôm trước phàn nàn là cùng 1 bài toán mà 2 thầy cô lại ra 2 kết quả khác nhau, cháu hỏi lại gv thì sau 1 tuần vẫn chưa thấy hồi âm.
"Một trạm xá có 2 bác sĩ nam+ 3 yta nam + 5 yta nữ. Cần cử 1 nhóm gồm 3 người sao cho nhóm đó có cả bs cả yta , đồng thời có cả nam cả nữ. Hỏi có bao nhiêu cách chọn?"
Các cụ thông thái giúp em để em trả lời F1. Em xin cảm ơn ạ

Nhưng nếu làm cách khác:
+ Hoặc chọn 1BS nam + 1 ytá nữ + 1 ytá nam : có 2x5x3 = 30 cách
+ Hoặc chọn 1BS nam + 2 ytá nữ : có 2x10 = 20 cách
+ Hoặc chọn 2BS nam + 1 ytá nữ : có 2.10 = 20 cách
thì kết quả khác ( 30 + 20 + 20 =70! )
Vậy theo cụ sai chỗ nào?

 

[kiemtrapc]

Cách của cụ chính xác đến đoạn phải có 1 nam bsi và 1 nữ y tá ạ. Nhưng sau đó vde ở chỗ có lúc tính lặp 2 lần. Giả sử có 2 bsi là D1, D2 và 5 y tá là F1, F2, ... F5. Trong 10 cách chọn 1 nam bsi và 1 nữ y tá, gs 1 cách là D1, F1. Sau đó cụ chọn F2 cho ng thứ 3 còn lại, đc nhóm D1, F1, F2. Nhưng cách chọn 1 bsi và 1 nữ y tá sau đó lại tính lại D1, F2, rồi chọn ng 3 là F1, vậy là đếm trùng nhóm.

Theo em tính số cách chọn nhóm 3 người có 1 bsy và 2 y tá. Ta có tổ hợp chập 1 của 2 × tổ hợp chập 2 của 8 = 2x28= 56 cách chọn.

cách chọn nhóm 3 người có 2 bsy và 1 yta là 1x8=8 cách chọn.

Cách chọn nhóm 3 người có 1 basy và 2 ytá Nam= tổ hợp chập 1 của 2 x tổ hợp chập 2 của 3=2 x 3= 6 cách chọn

Cách chọn nhóm 3 người có 2 bsy và 1 y tá nam = 1x3= 3 cách chọn.

Vậy số c cách chọn theo đề bài là 56+8 - 6-3=5 5 cách ạ.

Đáp án::55 cách

Người còn lại là yta hay Bs đều thoat mãn. Nên Tổng 80 cụ ah

bài giải cụ đâu để em phản biện ợ. Không là em sai rồi cụ xin lỗi em đi

Bác nói đúng.


2 Bs nam và 1 y tá nữ chỉ có 5 trường hợp chứ không phải 10, vì không quan tâm đến thứ tự Bs nam (nếu Bs nam xếp đầu làm trưởng đoàn thì lại là 10 trường hợp).


1 Bs nam và 2 y tá nữ: đây thực ra là chọn tổ hợp chập 2 của 5, tức là có bao nhiêu cách chọn 2 phần tử từ tập hợp 5. Được kết quả bao nhiêu nhân 2, vì có 2 Bs nam.


Thế thôi.

3 trg hợp:

- 2 bác sỹ, 1 y tá nữ: 2C2.5C1=5.

- 1 bs, 2 y tá nữ: 2C1.5C2=20.

- 1 bs, 1 t tá nam, 1 y tá nữ: 2C1.3C1.5C1=30.

Tổng: 55.

+ Hoặc chọn 1BS nam + 1 ytá nữ + 1 ytá nam : có 2x5x3 = 30 cách

+ Hoặc chọn 1BS nam + 2 ytá nữ : có 2x5x4 = 40 cách

+ Hoặc chọn 2BS nam + 1 ytá nữ : có 1x5 = 5 cách


Tổng: 30 + 40 + 5 = 75.

Em xin tóm tắt lại 2 cách giải cho bài toán trên như sau:

Lời giải 1:

Hoặc chọn 2 bs nam + 1 yta nữ: Có 1 x 5 = 5 cách

Hoặc chọn 1 bs nam + y tá nữ + y tá nam: có 2x 5 x 3 = 30 cách

Hoặc chọn 1 bs nam + 2 y tá nữ : có 2 x 10 = 20 cách

Áp dụng quy tắc cộng thì số cách là : 55 cách

Lời giải 2:

Thực hiện lần lượt các bước sau:

Bước 1: chọn 1 trong số 2 bác sỹ nam : có 2 cách

Bước 2: chọn 1 trong số 5 tá nữ : có 5 cách

Bước 3: chọn 1 người bất kỳ trong số 8 người còn lại ( còn lại 1bs + 4 yta nữ + 2 y tá nam) : có 8 cách

Áp dụng quy tắc nhân : có 2 x 5 x 8 = 80 cách
Các cụ giúp em thì giúp cho trót! Em muốn hỏi cách nào đúng?
Đa số các cụ đều ra kết quả 55. Vậy lời giải cho kết quả 2 thì sai chỗ nào ạ?

 

[icyeyes]

Em xin giới thiệu là cách ra 80 đã đếm trùng nhóm như sau:
Gọi 2 nam bác sĩ là Hùng, Quân. Gọi 5 nữ yta là Mai, Lan, Cúc, Trúc, Điệp.
Theo bước 1, 2 cụ đã chọn ra đc 1 nam bsi và 1 nữ yta. Có 10 cách, đúng. Xét 1 trong 10 cách này là cụ chọn Hùng, Mai.
Bước 3 cụ chọn ng còn lại trong 8 ng. Một trong 8 cách đó là chọn Lan. Ok, cụ đc nhóm là Hùng, Mai, Lan.

Tiếp, cụ chọn 1 nam bsi, 1 nữ yta. Lần này trong 10 cách, cụ có cách chọn Hùng, Lan.
Có Hùng, Lan rồi, cụ làm bước 3, chọn 1 trong 8 ng còn lại, trong đó có cách chọn Mai. Vậy đc nhóm: Hùng, Lan, Mai.

Vừa xong cụ đã đếm nhóm này 2 lần, nhưng thực ra chỉ có 1 nhóm. Vậy là đếm trùng lặp.

 

[Mơ Mer]

Có 2 cách chọn người thứ nhất là bác sĩ nam, với mỗi cách chọn bác sĩ nam sẽ có 5 cách chọn người thứ hai là y tá nữ.
Như thế đã thỏa mãn đề bài ra là có cả bác sĩ, y tá, cả nam cả nữ.
Như vậy người thứ 3 chọn như nào cũng được trong 8 người còn lại (1 bác sĩ nam, 5 y tá nam, 2 y tá nữ).

Vậy số cách chọn là: 2*5*8 = 80 cách.

Update:
Nhưng như vậy sẽ có một số trường hợp trùng nhau do cùng 1 người nhưng đứng ở 2 vị trí.
Hic hic em sai rồi.
Chắc phải chia 3 trường hợp nhóm mà tính thôi

 

[kiemtrapc]

Em xin giới thiệu là cách ra 80 đã đếm trùng nhóm như sau:
Gọi 2 nam bác sĩ là Hùng, Quân. Gọi 5 nữ yta là Mai, Lan, Cúc, Trúc, Điệp.
Theo bước 1, 2 cụ đã chọn ra đc 1 nam bsi và 1 nữ yta. Có 10 cách, đúng. Xét 1 trong 10 cách này là cụ chọn Hùng, Mai.
Bước 3 cụ chọn ng còn lại trong 8 ng. Một trong 8 cách đó là chọn Lan. Ok, cụ đc nhóm là Hùng, Mai, Lan.

Tiếp, cụ chọn 1 nam bsi, 1 nữ yta. Lần này trong 10 cách, cụ có cách chọn Hùng, Lan.
Có Hùng, Lan rồi, cụ làm bước 3, chọn 1 trong 8 ng còn lại, trong đó có cách chọn Mai. Vậy đc nhóm: Hùng, Lan, Mai.

Vừa xong cụ đã đếm nhóm này 2 lần, nhưng thực ra chỉ có 1 nhóm. Vậy là đếm trùng lặp.

Đã chọn Hùng, Mai ở bước 1 và 2 rồi thì sang bước 3 làm gì còn mà chọn lặp lại được hả cụ?
Cách đếm ra kết quả 80 là do em thấy GV dạy F1 như vậy và làm tương tự. Đấy là cách người ta đếm sử dụng quy tắc nhân đấy cụ ạ
1. QUY TẮC CỘNG:
'Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + ncách thực hiện.
2. QUY TẮC NHÂN:
" Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m × n cách hoàn thành công việc".

• Quy tắc cộng được thực hiện khi các hành động là độc lập (hiểu theo nghĩa "hoặc")
• Quy tắc nhân được thực hiện khi các hành động là liên tiếp (hiểu theo nghĩa "và")
• Quy tắc cộng và quy tắc nhân có thể mở rộng cho nhiều trường hợp.

http://vi.kien-thuc.wikia.com/wiki/Quy_tắc_đếm

 

[kiemtrapc]

Có 2 cách chọn người thứ nhất là bác sĩ nam, với mỗi cách chọn bác sĩ nam sẽ có 5 cách chọn người thứ hai là y tá nữ.
Như thế đã thỏa mãn đề bài ra là có cả bác sĩ, y tá, cả nam cả nữ.
Như vậy người thứ 3 chọn như nào cũng được trong 8 người còn lại (1 bác sĩ nam, 5 y tá nam, 2 y tá nữ).

Vậy số cách chọn là: 2*5*8 = 80 cách.

Update:
Nhưng như vậy sẽ có một số trường hợp trùng nhau do cùng 1 người nhưng đứng ở 2 vị trí.
Hic hic em sai rồi.
Chắc phải chia 3 trường hợp nhóm mà tính thôi

Vấn đề em muốn hỏi là cách nào đúng? Nếu cách này đúng thì sao cách kia lại sai (Vì 2 cách 2 kết quả mà cụ)

 

[IP man]

Đã chọn Hùng, Mai ở bước 1 và 2 rồi thì sang bước 3 làm gì còn mà chọn lặp lại được hả cụ?
Cách đếm ra kết quả 80 là do em thấy GV dạy F1 như vậy và làm tương tự. Đấy là cách người ta đếm sử dụng quy tắc nhân đấy cụ ạ
1. QUY TẮC CỘNG:
'Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + ncách thực hiện.
2. QUY TẮC NHÂN:
" Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m × n cách hoàn thành công việc".

• Quy tắc cộng được thực hiện khi các hành động là độc lập (hiểu theo nghĩa "hoặc")
• Quy tắc nhân được thực hiện khi các hành động là liên tiếp (hiểu theo nghĩa "và")
• Quy tắc cộng và quy tắc nhân có thể mở rộng cho nhiều trường hợp.

http://vi.kien-thuc.wikia.com/wiki/Quy_tắc_đếm

Em thấy cụ chưa hiểu về bản chất mà giải toán máy móc quá.

Lời giải 2 đã có nhiều phân tích là sai vì bị trùng lặp.

Ví dụ:
Ở bộ đếm thứ nhất:
- Bác sĩ chọn 1 trong 2: chọn Hùng
- Y tá nữ chọn 1 trong 5: chọn Mai
- Người còn lại chọn 1 trong 8: chọn Quân (bác sĩ)
-> ta có nhóm 1: Hùng + Mai + Quân

Ở bộ đếm thứ hai:
- Bác sĩ chọn 1 trong 2: chọn Quân
- Y tá nữ chọn 1 trong 5: chọn Mai
- Người còn lại chọn 1 trong 8: chọn Hùng.
-> có nhóm 2: Quân + Mai + Hùng

Nhóm 1 và nhóm 2 trùng nhau.
Đây là 1 ví dụ về lặp thôi, chứ trong cách này còn lặp nhiều.

 

[hoangmanhquang]

Em xin tóm tắt lại 2 cách giải cho bài toán trên như sau:

Lời giải 1:

Hoặc chọn 2 bs nam + 1 yta nữ: Có 1 x 5 = 5 cách

Hoặc chọn 1 bs nam + y tá nữ + y tá nam: có 2x 5 x 3 = 30 cách

Hoặc chọn 1 bs nam + 2 y tá nữ : có 2 x 10 = 20 cách

Áp dụng quy tắc cộng thì số cách là : 55 cách

Lời giải 2:

Thực hiện lần lượt các bước sau:

Bước 1: chọn 1 trong số 2 bác sỹ nam : có 2 cách

Bước 2: chọn 1 trong số 5 tá nữ : có 5 cách

Bước 3: chọn 1 người bất kỳ trong số 8 người còn lại ( còn lại 1bs + 4 yta nữ + 2 y tá nam) : có 8 cách

Áp dụng quy tắc nhân : có 2 x 5 x 8 = 80 cách
Các cụ giúp em thì giúp cho trót! Em muốn hỏi cách nào đúng?
Đa số các cụ đều ra kết quả 55. Vậy lời giải cho kết quả 2 thì sai chỗ nào ạ?

Cách 1 đúng (như em đã giải ). Cách 2 sai, và sai ở chỗ đếm lặp. Cụ thể, nếu nhìn vào phân nhóm của Cách 1, các nhóm có 2 bác sỹ nam hoặc 2 y tá nữ sẽ được đếm 2 lần (như bác IP Man giảng ở trên). Lấy số của Cách 2 trừ đi các trường hợp lặp này (80 - 5 - 20) sẽ ra đáp số đúng ở Cách 1.

 

[vietnamcongtru]

Đáp án 55 là đúng. Nhưng ta phải có cách tổng quát để giải bài này chứ nhỉ. Lỡ đề bài ra: có 20 bác sĩ nam, 30 y tá nam, 50_y tá nữ; chọn 30 người sao cho có cả nam lẫn nữ, cả bác sĩ lẫn y tá...thì làm sao?
Em biết cách giải nhưng không nói đâu

 

[HUNGBDA79]

Chỉ có 2 nam bác sỹ và chỉ có 5 nữ y tá.
Nên nhóm 3 người bắt buộc phải có 1 nam bác sỹ cộng 1 nữ y tá. Người còn lại là bất kỳ ai còn lại.
Có 10 cách chọn nhóm 1 nam bác sỹ + 1 nữ y tá. Mỗi cách đó lại có 8 cách chọn nốt đồng đội.
Tổng số có 80 cách chọn nhóm 3 người thoả mãn đề bài.

(Nhà cháu quên hết kiến thức tổ hợp chỉnh hợp rồi, diễn vo cho nó nhanh)

Chập k của n phần tử jj đấy e quên mệ nó rồi

 

[Aziz Nesin]

Đáp án 55 là đúng. Nhưng ta phải có cách tổng quát để giải bài này chứ nhỉ. Lỡ đề bài ra: có 20 bác sĩ nam, 30 y tá nam, 50_y tá nữ; chọn 30 người sao cho có cả nam lẫn nữ, cả bác sĩ lẫn y tá...thì làm sao?
Em biết cách giải nhưng không nói đâu

Cách giải tổng quát là theo tính gián tiếp qua phần bù
Kiểu như đội OF gồm 1000 thành viên nhưng quá nhiều thành viêc có trym, thì thay vì cách đếm thành viên có trym cụ có thể đếm thành viên có bím . Xong lấy tổng trừ đi bím thì ra số trym

 

[Trục]

2*5*8= 80 cách chọn. (Cách chọn lớn nhất là cách đúng).
Giả thiết: 2*9*4=72 là số bé hơn lên không chọn.

F1 nhà em học lớp 11, hôm trước phàn nàn là cùng 1 bài toán mà 2 thầy cô lại ra 2 kết quả khác nhau, cháu hỏi lại gv thì sau 1 tuần vẫn chưa thấy hồi âm.
"Một trạm xá có 2 bác sĩ nam+ 3 yta nam + 5 yta nữ. Cần cử 1 nhóm gồm 3 người sao cho nhóm đó có cả bs cả yta , đồng thời có cả nam cả nữ. Hỏi có bao nhiêu cách chọn?"
Các cụ thông thái giúp em để em trả lời F1. Em xin cảm ơn ạ

Yếu tố đầu chọn bác sĩ, nên chỉ có hai cách chọn.
Yếu tố 2: chọn nữ trong nhóm nên chỉ có 5 cách chọn.
Yếu tố 3: cho đủ nhóm 3 người còn 3+4+1=8 cách chọn.

Kết quả: 2*5*8= 80 cách chọn.

 

[Trục]

Mợ có kết quả đúng mà.
Không có bất kỳ trường hợp nào trùng cả, vì nhân vật nam chính và nữ chính đã chọn đúng cách. Những nhân vật còn lại đã bị loại trừ trong cách chọn đã được loại bỏ và chỉ là nhân vật phụ trong khi chọn người thứ 3. Thể hiện trong phép trừ 2-1=1(bs) 5-1=4(yta nữ)và 3(yta nam) tổng của họ là 8.

Có 2 cách chọn người thứ nhất là bác sĩ nam, với mỗi cách chọn bác sĩ nam sẽ có 5 cách chọn người thứ hai là y tá nữ.
Như thế đã thỏa mãn đề bài ra là có cả bác sĩ, y tá, cả nam cả nữ.
Như vậy người thứ 3 chọn như nào cũng được trong 8 người còn lại (1 bác sĩ nam, 5 y tá nam, 2 y tá nữ).

Vậy số cách chọn là: 2*5*8 = 80 cách.

Update:
Nhưng như vậy sẽ có một số trường hợp trùng nhau do cùng 1 người nhưng đứng ở 2 vị trí.
Hic hic em sai rồi.
Chắc phải chia 3 trường hợp nhóm mà tính thôi

 

[suzu37]

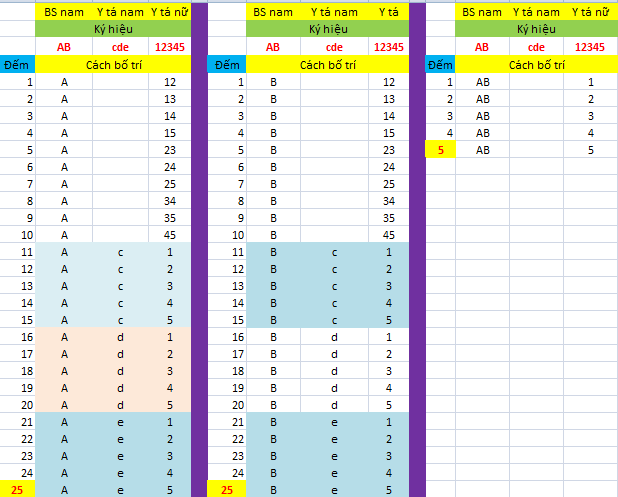
Vấn đề em muốn hỏi là cách nào đúng? Nếu cách này đúng thì sao cách kia lại sai (Vì 2 cách 2 kết quả mà cụ)

Bác xem em có kê thiếu tổ hợp nào không nhé.

Em ngồi rỗi làm bộ tổ hợp cho vui. Tổng là 55.

Nếu bác xác nhận cái ảnh của em thì tự khắc bài 80 kia sẽ thấy sai chỗ nào.

 

[kiemtrapc]

Bác xem em có kê thiếu tổ hợp nào không nhé.

Em ngồi rỗi làm bộ tổ hợp cho vui. Tổng là 55.

Nếu bác xác nhận cái ảnh của em thì tự khắc bài 80 kia sẽ thấy sai chỗ nào.

Cảm ơn cụ rất nhiều! Em cũng nghĩ kết quả 55 là đúng
Vấn đề là cách kia cũng khó chỉ ra chỗ sai bằng lập luận !
Em sẽ học cách cụ để từ ví dụ sai để lập luận ko áp dụng đc quy tắc nhân theo hướng dẫn của GV ạ

 

[kiemtrapc]

2*5*8= 80 cách chọn. (Cách chọn lớn nhất là cách đúng).
Giả thiết: 2*9*4=72 là số bé hơn lên không chọn.
Yếu tố đầu chọn bác sĩ, nên chỉ có hai cách chọn.
Yếu tố 2: chọn nữ trong nhóm nên chỉ có 5 cách chọn.
Yếu tố 3: cho đủ nhóm 3 người còn 3+4+1=8 cách chọn.

Kết quả: 2*5*8= 80 cách chọn.

Cách này sai nhưng em chưa lập luận để chỉ ra chỗ sai đc cụ ạ