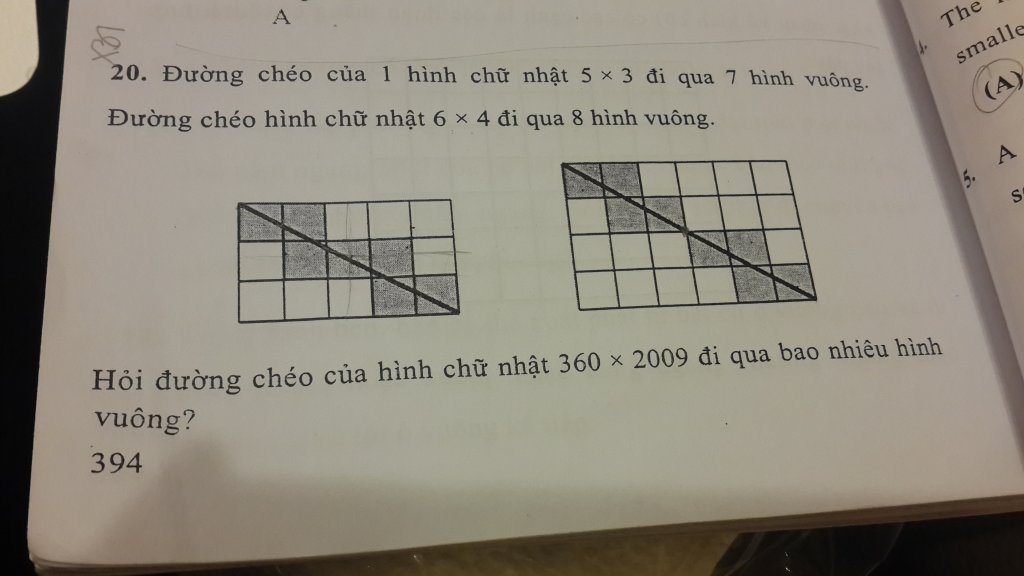
Bài ô vuông
Từ "cột đứng" và "dòng ngang" em nói đưới đây hiểu là các đường kẻ lưới đứng và ngang
Do 2009 và 360 là nguyên tố cùng nhau nên trừ hai đỉnh thì đường chéo của hình chữ nhật sẽ không đi qua các đỉnh của các hình vuông nằm trong.
Nhing từ trái qua, đường chéo bị các cột đứng chia thành 2009 đoạn nhỏ, mỗi đoạn nhỏ nhìn từ dưới lên thì chỉ có hai hai khả năng: hoặc nó nằm hoàn toàn trong một hình vuông hoặc bị cắt ngang bởi một trong (360-1) dòng ngang, và có (360-1) lần cắt như vậy, có thêm tương ứng (360-1) hình vuông
Vậy sẽ có 2009 +(360-1) = 2368 hình vuông.
Trường hợp tổng quát, m x n ô vuông
- m và n nguyên tố cùng nhau: làm như trên kết quả là m+n-1
- m và n có ước chung lớn nhất là p>1, tức m = p x M và n = p x N với M và N nguyên tố cùng nhau
Quan trọng nhất ở đây là hiểu sau MxN ô thi đường chéo lại đi qua 2 đỉnh hình chữ nhật tạo bởi MxN ô đó, và có p lần như vậy.
Vậy kết quả là (M+N-1) x p = m+n-p