[Funland] Một bài toán cấp 2 nhờ các cụ thông thái xem giúp

[Aziz Nesin]

Cụ nào chuyên dạy toán cấp 2 xem giúp e cách giải và trình bày cho các cháu c2 hiểu với ạ

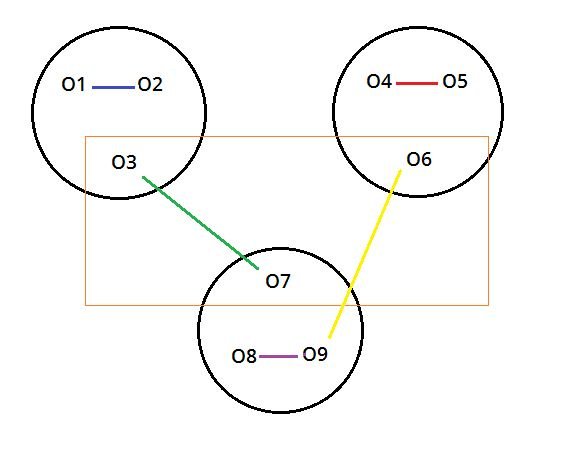
Trong cuộc hội thảo quốc tế có 9 nhà khoa học tham dự. Người ta nhận thấy rằng cứ 3 đại biểu bất kỳ luôn có 2 đại biểu nói chuyện được với nhau. Ngoài ra mỗi đại biểu biết không quá 3 thứ tiếng.
Chứng minh rằng luôn tìm được 3 đại biểu biết cùng một thứ tiếng.

 

[langtoilangtoi]

Để chứng minh điều này, ta có thể sử dụng định lí Ramsey như sau:

Với mỗi đồ thị đơn vô hướng đầy đủ có 9 đỉnh và 2 màu, ta có thể tìm được ít nhất một đường đi độ dài 3 đơn vị có tất cả các đỉnh cùng màu hoặc có ít nhất 3 đỉnh thuộc cùng một màu.

Để áp dụng định lí này, ta gán mỗi đỉnh đại diện cho một nhà khoa học, và gán màu đỏ cho các đại biểu không thể nói chuyện với nhau, và gán màu xanh cho các đại biểu có thể nói chuyện được với nhau.

Theo giả thiết của đề bài, với mỗi tập 3 đại biểu bất kỳ, luôn có ít nhất 2 đại biểu nói chuyện được với nhau. Điều này tương đương với việc đồ thị của chúng ta không chứa bất kỳ tam giác đỏ nào. Do đó, theo định lí Ramsey, ta sẽ tìm được một đường đi độ dài 3 đơn vị có tất cả các đỉnh cùng màu hoặc có ít nhất 3 đỉnh thuộc cùng một màu. Trong cả hai trường hợp, ta đều sẽ tìm được 3 đại biểu biết cùng một thứ tiếng, vì các đại biểu trong cùng một nhóm có thể nói chuyện được với nhau. Do đó, chúng ta đã chứng minh được rằng luôn tìm được 3 đại biểu biết cùng một thứ tiếng.

(Open AI cho biết)

 

[New car 2023]

Để chứng minh điều này, ta có thể sử dụng định lí Ramsey như sau:

Với mỗi đồ thị đơn vô hướng đầy đủ có 9 đỉnh và 2 màu, ta có thể tìm được ít nhất một đường đi độ dài 3 đơn vị có tất cả các đỉnh cùng màu hoặc có ít nhất 3 đỉnh thuộc cùng một màu.

Để áp dụng định lí này, ta gán mỗi đỉnh đại diện cho một nhà khoa học, và gán màu đỏ cho các đại biểu không thể nói chuyện với nhau, và gán màu xanh cho các đại biểu có thể nói chuyện được với nhau.

Theo giả thiết của đề bài, với mỗi tập 3 đại biểu bất kỳ, luôn có ít nhất 2 đại biểu nói chuyện được với nhau. Điều này tương đương với việc đồ thị của chúng ta không chứa bất kỳ tam giác đỏ nào. Do đó, theo định lí Ramsey, ta sẽ tìm được một đường đi độ dài 3 đơn vị có tất cả các đỉnh cùng màu hoặc có ít nhất 3 đỉnh thuộc cùng một màu. Trong cả hai trường hợp, ta đều sẽ tìm được 3 đại biểu biết cùng một thứ tiếng, vì các đại biểu trong cùng một nhóm có thể nói chuyện được với nhau. Do đó, chúng ta đã chứng minh được rằng luôn tìm được 3 đại biểu biết cùng một thứ tiếng.

(Open AI cho biết)

Bác bẩu cậu Open AI dịch ra tiếng Việt giùm cái.
Thank you.

 

[QDV2012]

Khả năng cao là biết cùng tiếng Anh hoặc đại biểu quốc hội chắc chắn biết tiếng Việt rồi

Just for fun em hóng các cụ chuyên toán vào giải thích

 

[langtoilangtoi]

Bác bẩu cậu Open AI dịch ra tiếng Việt giùm cái.
Thank you.

Đây là toán rời rạc mà các cụ học CNTT phải học năm thứ 3 thì phải. E khá ức chế khi đọc toán cấp 2,3 đưa khá nhiều kiến thức ĐH vào ở dạng này. Chắc mục tiêu phân loại học sinh, nhưng các phụ huynh học ngày trước rất khó tiếp cận để dạy con cái.

 

[j23]

Bài này chắc dùng biểu đồ Ven, còn chi tiết thì em nhường cụ dưới
Thằng con em hồi lớp 4 có học nhưng là dạng sơ cấp, hình như là nói tiếng Anh Pháp Trung chứ ko kiểu tù mù như đề này

 

[New car 2023]

Đây là toán rời rạc mà các cụ học CNTT phải học năm thứ 3 thì phải. E khá ức chế khi đọc toán cấp 2,3 đưa khá nhiều kiến thức ĐH vào ở dạng này. Chắc mục tiêu phân loại học sinh, nhưng các phụ huynh học ngày trước rất khó tiếp cận để dạy con cái.

Mục tiêu là nhồi nhét thôi bác.
Còn tại sao cứ phải nhồi và nhét thì tôi chịu.

 

[firstXpan]

Bài này theo em sẽ áp dụng nguyên lý diricle. nội dung nguyên lý như sau:
Có 7 con thỏ nhốt trong 2 chuồng, luôn tồn tại ít nhất một chuồng chứa 4 con thỏ.
Áp dụng vào bài trên thế nào để em nghĩ tiếp ạ.

 

[vanhai493]

Giả sử có 9 đại biểu A1, A2, A3, A4, A5, A6, A7, A8 và A9. Ta chứng minh rằng luôn tìm được 3 đại biểu biết cùng một thứ tiếng.

Để chứng minh điều này, ta sử dụng phương pháp giả định và phản chứng như sau:

• Giả định rằng không có bất kỳ nhóm đại biểu nào biết cùng một thứ tiếng.
• Theo giả định này, mỗi đại biểu có thể biết tối đa 3 thứ tiếng và cứ 3 đại biểu bất kỳ thì luôn có ít nhất 2 đại biểu biết cùng một thứ tiếng.
• Ta chia 9 đại biểu thành 3 nhóm 3 đại biểu. Theo giả định ban đầu, ta có thể xếp các đại biểu vào các nhóm sao cho không có 2 đại biểu nào biết cùng một thứ tiếng trong cùng một nhóm.
• Xét nhóm đại biểu B1 = {A1, A2, A3}. Theo giả định, không có 2 đại biểu nào biết cùng một thứ tiếng trong B1. Vậy mỗi đại biểu trong B1 biết tối đa 3 thứ tiếng, và do đó B1 phải bao gồm ít nhất 2 đại biểu biết cùng một thứ tiếng.
• Tương tự, xét nhóm đại biểu B2 = {A4, A5, A6} và nhóm đại biểu B3 = {A7, A8, A9}. Từ đó suy ra, trong 3 nhóm đại biểu này phải có ít nhất 1 nhóm đại biểu có ít nhất 2 đại biểu biết cùng một thứ tiếng.
• Điều này phản chứng với giả định ban đầu rằng không có bất kỳ nhóm đại biểu nào biết cùng một thứ tiếng. Vậy giả định này là sai, và ta có thể luôn tìm được 3 đại biểu biết cùng một thứ tiếng trong cuộc hội thảo quốc tế này.

Screenshot

Captured with Lightshot

prnt.sc

 

[j23]

Bài này theo em sẽ áp dụng nguyên lý diricle. nội dung nguyên lý như sau:
Có 7 con thỏ nhốt trong 2 chuồng, luôn tồn tại ít nhất một chuồng chứa 4 con thỏ.
Áp dụng vào bài trên thế nào để em nghĩ tiếp ạ.

À hóa ra là Dirichlet, dạng toán Thỏ - Lồng, ngày xưa học chuyên toán lớp 7, môn này em toàn 2-3 điểm

 

[Dacia90]

Cấp 2 thì chia nhóm cụ thể ra. Ngẫu nhiên 3 nhóm, lọc ra 3 ông không hiểu ở mỗi nhóm. 3 ông này bắt buộc phải nói được với nhau, không thì đi hội thảo QT làm gì?

 

[LuckyCar]

Ơ, cấp 1 có dạng này rồi á, tụi nó làm nhoay nhoáy, con em thì khó quá bỏ qua.

 

[j23]

Ơ, cấp 1 có dạng này rồi á, tụi nó làm nhoay nhoáy, con em thì khó quá bỏ qua.

dạ ko phải cụ ạ, em nhầm, nó ko phải là Veen mà là toán rời tạc Dirichlet

 

[ong dat]

Mục tiêu là nhồi nhét thôi bác.
Còn tại sao cứ phải nhồi và nhét thì tôi chịu.

Nhồi nhét để thể hiện mình cao siêu thì các cháu nó mới đăng ký học thêm !

 

[LuckyCar]

dạ ko phải cụ ạ, em nhầm, nó ko phải là Veen mà là toán rời tạc Dirichlet

Em không biết nó là dạng toán gì, nhưng em thấy chúng nó làm bạn A có mấy viên bi, bạn B mấy viên, hỏi có ít nhất bao nhiêu viên cùng màu, đại loại thế vì em không đọc kỹ.

 

[VuNgoanMuc]

Nó có phải giải theo nguyên lý này không nhỉ ? .. giờ toán cấp 2 em không tư duy được quên hết rồi

 

[firstXpan]

em mạo muội giải như sau, đúng sai mời các cụ chỉ giáo ạ.

Có 9 người ta gọi số thỏ là 9
2 đại biểu nói chuyện được với nhau nhóm thành các nhóm nên ta chọn số lồng là 9/2=4 lồng(hoặc nhóm)
Theo cụ Đi dép lê thì: Tồn tại ít nhất 1 nhóm có 3 con thỏ.

Hay là luôn tồn tại một nhóm có 3 người có thể nói chuyện với nhau biết cùng một ngoại ngữ. Nên ta có điều phải chứng minh (Theo giả thuyết cứ 3 đại biểu bất kỳ luôn có 2 đại biểu nói chuyện được với nhau có nghĩa là luôn có 1 cụ có thể nhồi vào một nhóm nào đó)

 

[Aziz Nesin]

Để chứng minh điều này, ta có thể sử dụng định lí Ramsey như sau:

Với mỗi đồ thị đơn vô hướng đầy đủ có 9 đỉnh và 2 màu, ta có thể tìm được ít nhất một đường đi độ dài 3 đơn vị có tất cả các đỉnh cùng màu hoặc có ít nhất 3 đỉnh thuộc cùng một màu.

Để áp dụng định lí này, ta gán mỗi đỉnh đại diện cho một nhà khoa học, và gán màu đỏ cho các đại biểu không thể nói chuyện với nhau, và gán màu xanh cho các đại biểu có thể nói chuyện được với nhau.

Theo giả thiết của đề bài, với mỗi tập 3 đại biểu bất kỳ, luôn có ít nhất 2 đại biểu nói chuyện được với nhau. Điều này tương đương với việc đồ thị của chúng ta không chứa bất kỳ tam giác đỏ nào. Do đó, theo định lí Ramsey, ta sẽ tìm được một đường đi độ dài 3 đơn vị có tất cả các đỉnh cùng màu hoặc có ít nhất 3 đỉnh thuộc cùng một màu. Trong cả hai trường hợp, ta đều sẽ tìm được 3 đại biểu biết cùng một thứ tiếng, vì các đại biểu trong cùng một nhóm có thể nói chuyện được với nhau. Do đó, chúng ta đã chứng minh được rằng luôn tìm được 3 đại biểu biết cùng một thứ tiếng.

(Open AI cho biết)

HS cấp 2 chưa học lí thuyết đồ thị cụ ạ

 

[Aziz Nesin]

Giả sử có 9 đại biểu A1, A2, A3, A4, A5, A6, A7, A8 và A9. Ta chứng minh rằng luôn tìm được 3 đại biểu biết cùng một thứ tiếng.

Để chứng minh điều này, ta sử dụng phương pháp giả định và phản chứng như sau:

• Giả định rằng không có bất kỳ nhóm đại biểu nào biết cùng một thứ tiếng.
• Theo giả định này, mỗi đại biểu có thể biết tối đa 3 thứ tiếng và cứ 3 đại biểu bất kỳ thì luôn có ít nhất 2 đại biểu biết cùng một thứ tiếng.
• Ta chia 9 đại biểu thành 3 nhóm 3 đại biểu. Theo giả định ban đầu, ta có thể xếp các đại biểu vào các nhóm sao cho không có 2 đại biểu nào biết cùng một thứ tiếng trong cùng một nhóm.
• Xét nhóm đại biểu B1 = {A1, A2, A3}. Theo giả định, không có 2 đại biểu nào biết cùng một thứ tiếng trong B1. Vậy mỗi đại biểu trong B1 biết tối đa 3 thứ tiếng, và do đó B1 phải bao gồm ít nhất 2 đại biểu biết cùng một thứ tiếng.
• Tương tự, xét nhóm đại biểu B2 = {A4, A5, A6} và nhóm đại biểu B3 = {A7, A8, A9}. Từ đó suy ra, trong 3 nhóm đại biểu này phải có ít nhất 1 nhóm đại biểu có ít nhất 2 đại biểu biết cùng một thứ tiếng.
• Điều này phản chứng với giả định ban đầu rằng không có bất kỳ nhóm đại biểu nào biết cùng một thứ tiếng. Vậy giả định này là sai, và ta có thể luôn tìm được 3 đại biểu biết cùng một thứ tiếng trong cuộc hội thảo quốc tế này.

Screenshot

Captured with Lightshot

prnt.sc

View attachment 7744843

Không xếp được như vậy cụ ạ. Vì giả thiết bài toán là "cứ 3 đại biểu bất kỳ luôn có 2 đại biểu nói chuyện được với nhau"

 

[Aziz Nesin]

Cấp 2 thì chia nhóm cụ thể ra. Ngẫu nhiên 3 nhóm, lọc ra 3 ông không hiểu ở mỗi nhóm. 3 ông này bắt buộc phải nói được với nhau, không thì đi hội thảo QT làm gì?

1 trong 3 ông mà cụ lọc ra thì vẫn có thể nc với một ông nào đó trong số các ông còn lại bằng một thứ tiếng nào đó khác với thứ tiếng của các nhóm cụ đã chia ạ