Thằng bạn em nó trả lời là chồng thêm 50 tầng nữa thì sập nhà rồi ạ, tính làm gì nữaDiện tích sử dụng hay mặt bằng cụ??
-
[Xe Của Năm 2026] Bình chọn Xe Của Năm 2026
[Funland] Bài thi thử lớp 5,mời các cụ thẩm câu trả lời
- Thread starter haidongtay
- Ngày gửi
Đúng rồi còn gì, lúc dó là hình tứ giác thôi.Em thấy trả lời thế này cũng đúng sao lại sai được nhỉ??

- Biển số
- OF-26254
- Ngày cấp bằng
- 23/12/08
- Số km
- 3,412
- Động cơ
- 512,366 Mã lực
Em văn dốt võ dát nhưng mạn phép bẻ lái cụ bằng chính hình của cụ.Câu trả lời của bạn học sinh lớp 5 này là SAI.
Đề bài hỏi về DIỆN TÍCH của hình vuông ban đầu sẽ THAY ĐỔI thế nào ?
Bạn học sinh lại hiểu rằng cái hình vuông sau khi tăng MỘT cạnh lên hai lần, VẪN PHẢI LÀ HÌNH VUÔNG.
Thực tế hình vuông sau khi tăng độ dài MỘT cạnh lên hai lần, sẽ trở thành hình tứ giác có một góc vuông.
Ở trình độ lớp 5 chỉ cần trả lời : DIỆN TÍCH TĂNG LÊN là đạt yêu cầu.
-------------
Ở trình độ cao hơn, có thể áp dụng công thức Heron để tính :
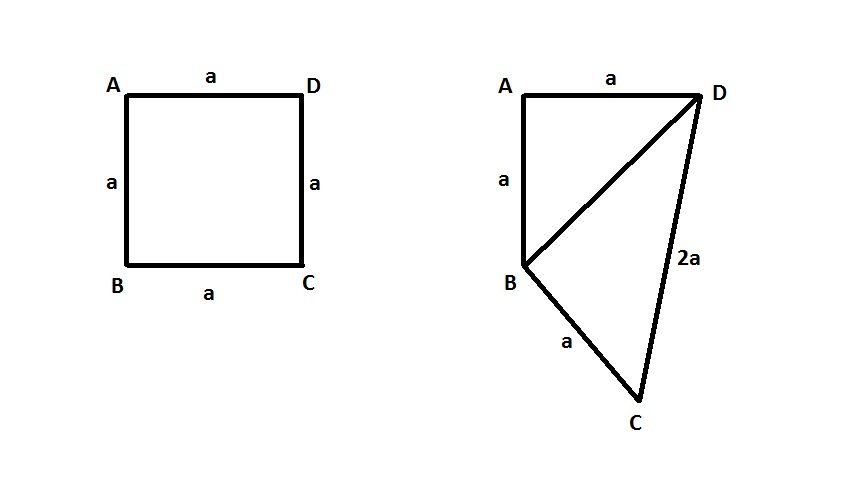
Từ hình vuông ban đầu (bên trái), sau khi tăng độ dài một cạnh lên hai lần, sẽ có hình tứ giác có một góc vuông (bên phải).
Diện tích hình tứ giác có một góc vuông (bên phải) là tổng diện tích của hai tam giác ABD và BCD.
1. Diện tích tam giác ABD = (a x a)/2
2. Diện tích tam giác BCD (theo công thức Heron) sẽ là : căn bậc hai của p(p - BC)(p - CD)(p - BD)
Trong đó p là nửa chu vi tam giác BCD.
Còm này cháu sai rồi ạ, cháu đã rút lại và thay bằng còm #135.Em văn dốt võ dát nhưng mạn phép bẻ lái cụ bằng chính hình của cụ.

- Biển số
- OF-14218
- Ngày cấp bằng
- 23/3/08
- Số km
- 9,167
- Động cơ
- -110,668 Mã lực
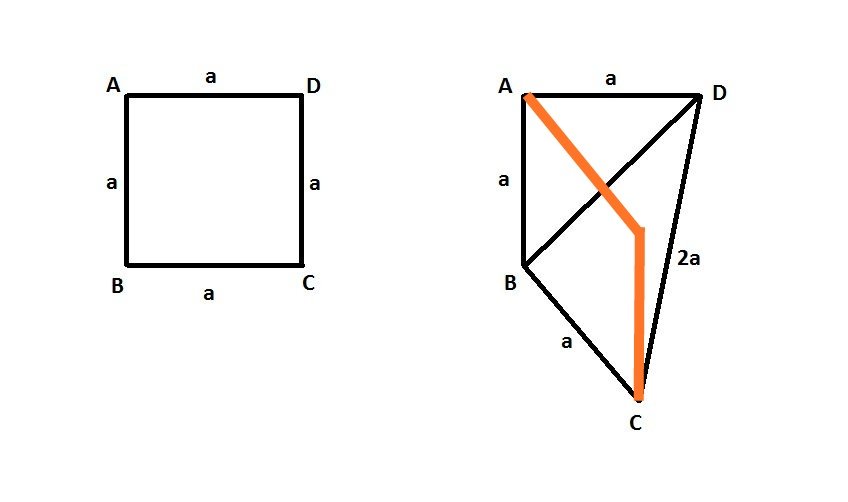
Cái này thì chưa chắc nhé cụ. Cụ có thể bóp hình cho diện tích bé đi mà vẫn giữ được 3 cạnh bằng nhau và cạnh thứ tư gấp đôi cạnh còn lại.Cháu giữ lại một góc vuông để mọi người dễ hình dung, khi MỘT CẠNH của hình vuông tăng chiều dài lên gấp hai lần, thì hình vuông đó sẽ biến thành hình tứ giác như thế nào (một số bác cứ nhầm lẫn là hình thang).
Tất nhiên là khi tăng chiều dài MỘT CẠNH của hình vuông, có thể thu được nhiều tứ giác không xác định. Nhưng dù là hình dạng như thế nào, thì diện tích vẫn LUÔN TĂNG LÊN (và đề bài cũng chỉ yêu cầu học sinh trình độ lớp 5 như vậy thôi : DIỆN TÍCH TĂNG LÊN).
Do đó, bài ko chặt chẽ.
Lớp 5 thì tuần lễ thứ 18 mới học đến hình thang (cuối học kỳ I), trừ khi trường F1 nhà bác dạy chương trình nhanh hơn các trường khác, thì mới giải được ạ.Để tối về em hỏi con em đang học lớp 5 xem nó có giải được ko. Đáp án bài này là 1,5 lần. Do chỉ có một cạnh tăng gấp đôi nên hình đó thành hình thang (đề không nói đó là hình vuông) có diện tích gấp 1,5 lần hình vuông ban đầu (tương đương 1 hình vuông + 1 tam giác vuông cân có 2 cạnh bằng cạnh của hình vuông ban đầu).
Đề bài nếu như thế này, thì không có vấn đề gì cả : "Diện tích của một hình vuông sẽ thay đổi như thế nào khi độ dài một cạnh của hình vuông đó tăng lên 2 lần, hình mới được tạo thành là hình thang"
Phải chăng cô giáo của F1 bác chủ thớt đã cắt đi cái đoạn nói về hình thang (vì học sinh chưa học) và cô nghĩ rằng việc cắt đi đó, không ảnh hưởng đến kết quả

- Biển số
- OF-14218
- Ngày cấp bằng
- 23/3/08
- Số km
- 9,167
- Động cơ
- -110,668 Mã lực
Nhà em đọc tuần tự nên giờ mới đọc còm này. Nhất trí là đề bài ko chặt chẽ. Có lẽ ý của cô là cạnh tăng 2 lần, diện tích tăng 4 lần, phù hợp tư duy lớp 5 khi vẽ hình.Sau khi tham khảo ý kiến của các cụ mợ trong thớt, có thể xảy ra 03 kết quả :
1. Nếu tứ giác mới được tạo ra khi độ dài MỘT cạnh của hình vuông tăng lên 2 lần, và tứ giác đó có 03 góc nhọn, thì DIỆN TÍCH GIẢM.
2. Nếu tứ giác mới được tạo ra khi độ dài MỘT cạnh của hình vuông tăng lên 2 lần, và tứ giác đó có ít hơn 03 góc nhọn, thì DIỆN TÍCH TĂNG.
3. Nếu tứ giác mới được tạo ra khi độ dài MỘT cạnh của hình vuông tăng lên 2 lần, và tứ giác đó vẫn là hình vuông cũ (chỉ kéo dài một cạnh), thì DIỆN TÍCH KHÔNG THAY ĐỔI.
Với một bài toán lớp 5 mà kết quả bất định như vậy thì đề bài sai (thừa từ "một"). Câu trả lời của em học sinh là chấp nhận được (với trình độ lớp 5 của em).
PS. Cháu xin rút lại ý kiến ở còm #31.
Vâng ạ, cháu viết sai ạ.Cái này thì chưa chắc nhé cụ. Cụ có thể bóp hình cho diện tích bé đi mà vẫn giữ được 3 cạnh bằng nhau và cạnh thứ tư gấp đôi cạnh còn lại.
Do đó, bài ko chặt chẽ.
- Biển số
- OF-14218
- Ngày cấp bằng
- 23/3/08
- Số km
- 9,167
- Động cơ
- -110,668 Mã lực
Em đã đọc bài cụ phân tích lại.Vâng ạ, cháu viết sai ạ.
Người ta hỏi nếu 1 cạnh hình vuông thay đổi thì diện tích của nó thay đổi ntn?
Chứ người ta không hỏi nó biến thành hình gì!
Chứ người ta không hỏi nó biến thành hình gì!
Dựng tam giác đều ABC, sau đó dựng tam giác đều ACD với D là điểm đối xứng với B qua AC, tiếp tục dựng tam giác đều CDE, với E là điểm đối xứng với A qua CD. Bây giờ ta có hình thang cân ADEB có 3 cạnh là a, 1 cạnh là 2a1. Bác chuẩn
2. Bác có thể chứng minh hai cạnh của hình tứ giác bác dựng, là song song với nhau không ạ ?
Mắt thường nhìn thì nó là hình thang, nhưng muốn chứng minh nó là hình thang thì bác phải chứng minh được hai cạnh song song với nhau ạ.
- Biển số
- OF-478190
- Ngày cấp bằng
- 21/12/16
- Số km
- 193
- Động cơ
- 197,710 Mã lực
- Tuổi
- 32
thành tứ giác dồiTheo em câu hỏi này là tư duy. Nếu 1 cạnh tăng 2 lần thì diện tích không thay đổi do 3 cạnh kia giữ nguyên.
Sent from my iPhone using Tapatalk
- Biển số
- OF-72542
- Ngày cấp bằng
- 10/9/10
- Số km
- 1,400
- Động cơ
- 421,996 Mã lực
... khi độ dài của "một cạnh" "của hình vuông "đó", em hiểu là chỉ 1 cạnh của hình vuông ban đầu kéo dài gấp 2, tức chỉ 1 cạnh kéo dài ra và diện tích hình vuông không đổi, đề bài ra không rõHình vuông khi 1 cạnh tăng lên thì mặc định các cạnh còn lại sẽ tăng như vậy để luôn đảm bảo nó vẫn là một hình vuông, câu hỏi cần kiến thức vững chắc.
- Biển số
- OF-417991
- Ngày cấp bằng
- 22/4/16
- Số km
- 1,527
- Động cơ
- 231,834 Mã lực
Cá nhân em thì thấy cô giáo tồi, đã ra đầu bài sai, không chặt chẽ bị học sinh phản bác thì chơi trò trả thù trừ điểm. Tất nhiên có những cuộc thi trả lời sai bị trừ điểm nhưng phải được ghi rõ để học sinh biết. Trong trường hợp này không ghi mà trừ nghéo của học sinh. Hồi con em học lớp 1 cô giáo cho bài tập về nhà la 3-5, con em không biết làm hỏi em, em bảo cô giáo cho đề sai. Hôm sau nó về bảo cô giáo xin lỗi đã cho đề sai. Em thỉnh thoảng cung cho đề sai cho nó bị nó kiện phải xin lỗi rối rít.
Bọn tư bản cũng cho ra đề sai trong những cuộc thi cực kỳ quan trọng là bình thường cho nên em bảo con em trước cuộc thi thấy đề bài có vẻ sai thì đừng mất thời gian vào câu đó hoặc sửa đầu bài vì câu đó kiểu gì cũng bị huỷ. Có đứa trẻ đã bị trượt oan vì mất quá nhiều tg vào những câu sai đề. Em ví dụ bằng tiếng Anh 1 câu toán trong kỳ thi lớp 6 vào 1 trường tư cực kỳ nổi tiếng của nước Anh:
James has 15 sweets in his pocket. He has 7 red sweets, 6 blue sweets, and 2 pink sweets. Without looking, he removes some sweets from his pocket and places them on the table. What is the smallest number of sweets he should remove to guarantee that he has at least one sweet of each colour?
Bọn tư bản cũng cho ra đề sai trong những cuộc thi cực kỳ quan trọng là bình thường cho nên em bảo con em trước cuộc thi thấy đề bài có vẻ sai thì đừng mất thời gian vào câu đó hoặc sửa đầu bài vì câu đó kiểu gì cũng bị huỷ. Có đứa trẻ đã bị trượt oan vì mất quá nhiều tg vào những câu sai đề. Em ví dụ bằng tiếng Anh 1 câu toán trong kỳ thi lớp 6 vào 1 trường tư cực kỳ nổi tiếng của nước Anh:
James has 15 sweets in his pocket. He has 7 red sweets, 6 blue sweets, and 2 pink sweets. Without looking, he removes some sweets from his pocket and places them on the table. What is the smallest number of sweets he should remove to guarantee that he has at least one sweet of each colour?
Cụ lại bị trừ tiếp 0.5 điểm ạ. Đã là hình vuông thì mặc định 4 cạnh nó phải bẳng nhau rồi mà cụ?Độ dài “mỗi” cạnh tăng 2 lần khác với độ dài “một” cạnh tăng 2 lần
Giáo viên bây giờ chấm điểm trừ lùi cụ ạ, mặc nhiên là 10, sai câu nào trừ lùi câu đó.Cụ gọi điện thoại hỏi Cô xem tại sao làm sai lại bị trừ điểm? Chả nhẽ thang điểm của cô có số âm?
- Biển số
- OF-391301
- Ngày cấp bằng
- 9/11/15
- Số km
- 2,229
- Động cơ
- 253,302 Mã lực
Câu trả lời đúng, cần tạo cho trẻ tư duy và nói đúng suy nghĩ của mình.
Em chỉ nói “mỗi” khác “một” thôi, cụ hiểu ý em chứCụ lại bị trừ tiếp 0.5 điểm ạ. Đã là hình vuông thì mặc định 4 cạnh nó phải bẳng nhau rồi mà cụ?
Em thì thiên hướng về việc 1 cạnh dài ra khi 3 cạnh còn lại có độ dài giữ nguyên sẽ biến hình vuông thành hình thang cân:

Hình thang này có diện tích bằng 3 lần tam giác đều có cạnh a, theo công thức diện tích tam giác đều cạnh a = a2 x (căn 3)/4
vậy nó có diện tích mới là:

Hình thang này có diện tích bằng 3 lần tam giác đều có cạnh a, theo công thức diện tích tam giác đều cạnh a = a2 x (căn 3)/4
vậy nó có diện tích mới là:
Câu trả lời của bạn học sinh lớp 5 này là SAI.
Đề bài hỏi về DIỆN TÍCH của hình vuông ban đầu sẽ THAY ĐỔI thế nào ?
Bạn học sinh lại hiểu rằng cái hình vuông sau khi tăng MỘT cạnh lên hai lần, VẪN PHẢI LÀ HÌNH VUÔNG.
Thực tế hình vuông sau khi tăng độ dài MỘT cạnh lên hai lần, sẽ trở thành hình tứ giác có một góc vuông.
Ở trình độ lớp 5 chỉ cần trả lời : DIỆN TÍCH TĂNG LÊN là đạt yêu cầu.
-------------
Ở trình độ cao hơn, có thể áp dụng công thức Heron để tính :

Từ hình vuông ban đầu (bên trái), sau khi tăng độ dài một cạnh lên hai lần, sẽ có hình tứ giác có một góc vuông (bên phải).
Diện tích hình tứ giác có một góc vuông (bên phải) là tổng diện tích của hai tam giác ABD và BCD.
1. Diện tích tam giác ABD = (a x a)/2
2. Diện tích tam giác BCD (theo công thức Heron) sẽ là : căn bậc hai của p(p - BC)(p - CD)(p - BD)
Trong đó p là nửa chu vi tam giác BCD.
Toán lớp 5 cũng căn não phéc nhỉ !
Thông tin thớt
Đang tải
Chia sẻ:
Bài viết mới
-
[Funland] Em có việc gấp xin nhờ các cụ ở Phương Liệt, HN
- Started by Boyngoan
- Trả lời: 4
-
[Funland] Từ năm 2026, hộ kinh doanh cho thuê nhà có doanh thu năm dưới 500 triệu được miễn thuế.
- Started by congthuong
- Trả lời: 1
-
[Funland] Thành lập Trường đại học Tâm Anh, đào tạo y khoa chuẩn quốc tế
- Started by hongan80
- Trả lời: 11
-
[Funland] Những điều không mong muốn xảy ra khi bước sang tuổi 50.
- Started by Lão Còi
- Trả lời: 29
-
[Funland] Người dân được giám sát CSGT thông qua những hình thức nào?
- Started by letrungdungvn
- Trả lời: 5
-
[Funland] Nhìn lại 2025, các cụ tiếc nhất điều gì? Điều muốn làm mà chưa làm dc ấy ạ!
- Started by Đừng sợ
- Trả lời: 26
-
[Funland] Em hỏi cách liên hệ Zalo để lấy lại tiền nếu bị hủy tài khoản
- Started by Mợ toét 2710
- Trả lời: 26
-
[Funland] Quân đội Trung Quốc đăng video cảnh tượng thành phố Đài Bắc
- Started by superman901
- Trả lời: 23
-
-
[Funland] 31/12/2025 - Tiến độ Đường trục phía Nam Hà Nội
- Started by sao_moc
- Trả lời: 4


