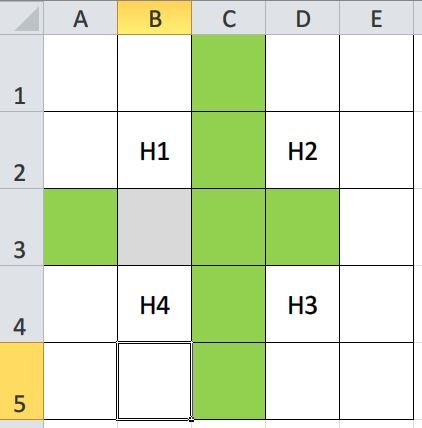
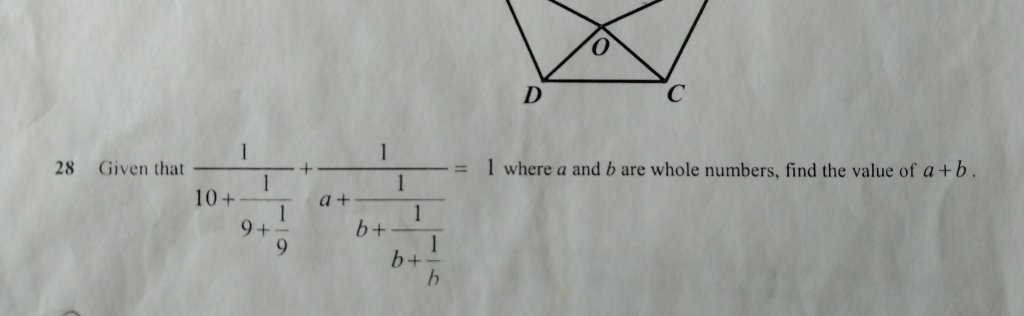21> Các đáp án 7 ô ở trên đều sai. Em cũng không nghĩ ra được đáp án 7 ô, chỉ nghĩ ra đáp án 8 ô thôi.
. . x . .
. . x . .
x x . x x
. . x . .
. . x . .
28> Quy đồng để tính cục bên trái trước
Đặt A1 = 9+1/9 = 82/9
Đặt A2 = 10 + 1/A1 = 10 + 9/82 = 829/82
L = 1/A2 = 82 / 829
Suy ra cục bên phải
R = 1 - L = 747/829
Quy đồng cục bên phải:
B1 = b+1/b = (b^2 + 1) / b
B2 = b+ 1/B1 = b + b / (b^2+1) = (b^3 + 2b) / (b^2 +1)
B3 = a + 1/B2 = a + (b^2+1) / (b^3+2b) = (ab^3 + 2ab + b^2 + 1) / (b^3 + 2b) = 1/R = 829 / 747
Nhìn cái phương trình thì ghê vậy thôi, nhưng đề bài đã cho: a, b là 2 số nguyên. Nếu để ý 2 hệ số cao nhất là ab^3 và b^3, và kết quả 829/747 xấp xỉ bằng 1, thì ta có thể kết luận ngay a = 1.
Thay a = 1 vào phương trình, ta có
(b^3 + 2b + b^2 + 1) / (b^3 + 2b) = 829/747
-> (b^2 + 1) / (b^3 + 2b) = 82/747
-> (b^2 + 1) / [b(b^2 + 2)] = 82/747
Dự đoán: (b^2 + 1) / [b(b^2 + 2)] có kết quả xấp xỉ 1/b, và 82/747 cũng xấp xỉ 1/9. Vậy khả năng cao b cũng sẽ bằng 9.
Thay b = 9 để kiểm tra lại thì ra kết quả đúng.
(Vì đây là bài tiểu học nên em mới giải kiểu này, chứ không thì em giải luôn phương trình bậc 3 cho nhanh)
-> a+b = 10.
P/S: bài 20 chỉ cần 1 nhát cắt thôi nhé. Cắt ra thành 6 đoạn 1, 2, 4, 8, 16, 32. Vì đó là sợi dây, có thể uốn lượn tùy ý, nên có thể cắt 1 phát 5 chỗ cùng lúc.