2 tam giác kia bằng nhau do Cạnh - góc - canh chứ sao lại đồng dạng nhỉ. NAB và IEB ấy.Lại mất tg rồi, hình như là 30 độ, dựng thêm hình tam giác đều là ra. Đây là tóm tắt lời giải
[Funland] Các cụ giỏi hình học lớp 8 giúp hộ cháu với
- Thread starter Quang Bo
- Ngày gửi
Em chỉ nhớ cái tam giác này khác đặc biệt, và thường kiểu gì cũng vẽ thêm tam giác đều, vì nó có góc 20 và 80, vừa đủ chênh lệch góc tam giác đều
- Biển số
- OF-533992
- Ngày cấp bằng
- 25/9/17
- Số km
- 6,620
- Động cơ
- 430,246 Mã lực
Tg NAB = Tg BEI chứ cụ?2 tam giác kia bằng nhau do Cạnh - góc - canh chứ sao lại đồng dạng nhỉ. NAB và IEB ấy.
E hóng
Chỉnh sửa cuối:
hình học thường này chưa phải là khó , hình học không gian mới khó vì nó cần thêm trí tưởng tượng . Khoe với các cụ trước e giải toán hình học không gian đúng đáp số nhưng cô giáo không hình dung ra được là tại sao lại đứng  , vd : tam giác hình tháp này thì 3 cạnh = nhau .
, vd : tam giác hình tháp này thì 3 cạnh = nhau .
 , vd : tam giác hình tháp này thì 3 cạnh = nhau .
, vd : tam giác hình tháp này thì 3 cạnh = nhau .sao e tính ra góc 50° các bác ạ
- Biển số
- OF-579316
- Ngày cấp bằng
- 15/7/18
- Số km
- 7,965
- Động cơ
- 1,084,926 Mã lực
Đề xuất của cụ làm lộ ra bài toán thuận mà bài toán này là bài toán nghịch.
E thử phát biểu bài toán thuận.
Cho hình thang cân BNEI có các góc đáy tại B, E = g = 20° và nhận BI, NE là phân giác; M là chân đường vuông góc hạ từ B xuống EI, BM cắt EI tại A. Cmr: h = BA/BN = 1.
Cm:
Ta có ^MNB = ^NBI + ^NIB= 3/2•g
-> ^MBN = 90° - 3/2•g = 90° - 30° = 60°.
Lớp 8: Vậy tam giác vuông MNB là 1/2 tam giác đều -> MB = 1/2BN
Mà AB = 2MB => h = AB/BN = 1 (dfcm)
Nhận xét: ở góc độ lớp 11 ta có: MB/BN = sin (^MNB) = sin (3/2•g)
-> h = AB/BN = 2•sin(3/2•g) (1)
Tức là với công thức (1) ta sẽ, biết g sẽ suy ra h (bài toán thuận), biết h sẽ suy ra g (bài toán nghịch type 1), biết h & g suy ra yếu tố còn lại (BE là phân giác góc NBI) (bài toán nghịch type 2)
Bài toán cụ thớt là bài toán ngược type 2 với h = 1 & g=20°.
Các cụ hoàn toàn có thể chế cháo thêm với g hoặc h bằng giá trị nào đó, để gen ra các bài toán thuận, nghịch khác.
E thử phát biểu bài toán thuận.
Cho hình thang cân BNEI có các góc đáy tại B, E = g = 20° và nhận BI, NE là phân giác; M là chân đường vuông góc hạ từ B xuống EI, BM cắt EI tại A. Cmr: h = BA/BN = 1.
Cm:
Ta có ^MNB = ^NBI + ^NIB= 3/2•g
-> ^MBN = 90° - 3/2•g = 90° - 30° = 60°.
Lớp 8: Vậy tam giác vuông MNB là 1/2 tam giác đều -> MB = 1/2BN
Mà AB = 2MB => h = AB/BN = 1 (dfcm)
Nhận xét: ở góc độ lớp 11 ta có: MB/BN = sin (^MNB) = sin (3/2•g)
-> h = AB/BN = 2•sin(3/2•g) (1)
Tức là với công thức (1) ta sẽ, biết g sẽ suy ra h (bài toán thuận), biết h sẽ suy ra g (bài toán nghịch type 1), biết h & g suy ra yếu tố còn lại (BE là phân giác góc NBI) (bài toán nghịch type 2)
Bài toán cụ thớt là bài toán ngược type 2 với h = 1 & g=20°.
Các cụ hoàn toàn có thể chế cháo thêm với g hoặc h bằng giá trị nào đó, để gen ra các bài toán thuận, nghịch khác.
Cụ Rivers làm đúng rùi, khó thế mà cũng nghĩ ra.
Chứng minh tam giác EIB = NBI thì nhanh hơn
Chỉnh sửa cuối:
à cụ trên đọc đề bài nhầm giống e, đọc nhầm AE=AB nên mới ra tam giác cân, và tính ra 50° thậtEm thấy sai sai mợ à EAB tại sao là tam giác cân được ạ
- Biển số
- OF-389654
- Ngày cấp bằng
- 30/10/15
- Số km
- 194
- Động cơ
- 239,261 Mã lực
- Tuổi
- 53
cám ơn cụ ạ !View attachment 7340021
Em giải thế này không biết có đúng không:
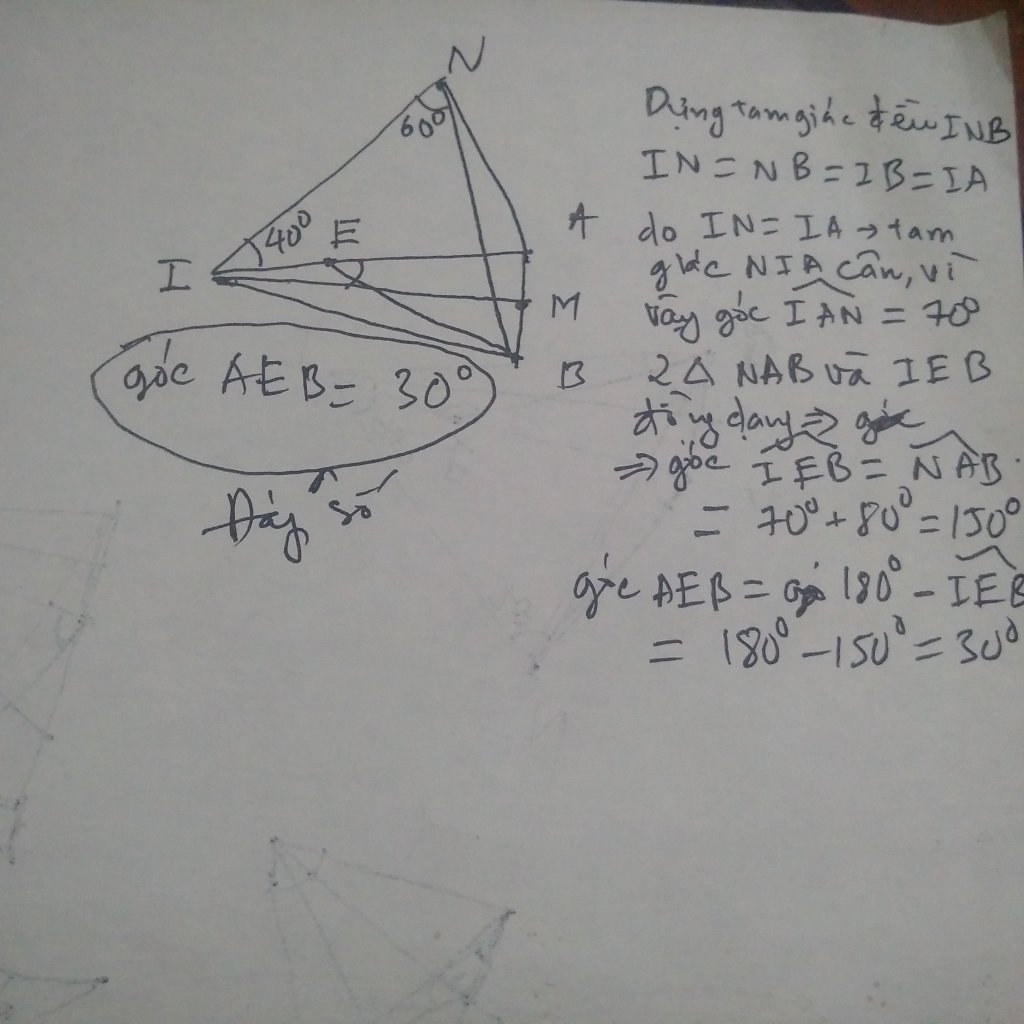
Giữa IM lấy điểm N sao cho NAM = 60° , vì d là trục đối xứng nên NBM cũng là 60° , tam giác ANB là tam giác cân, suy ra AN = AB = IE.
Ta so sánh 2 tam giác IAN và IBE có 2 cạnh AN = IE, IA = IB, 2 góc NAI = EIB = 20° cho nên 2 tam giác này bằng nhau, suy ra góc IBE = NIA = 10°
Vậy góc AEB = AIB + IBE = 20° + 10° = 30°
Chỗ so sánh tam giác bằng nhau kia em không chắc lắm vì kiến thức lâu lắm rồi chả biết có đúng không, cụ nào thấy sai vào phản biện giúp e.
- Biển số
- OF-389654
- Ngày cấp bằng
- 30/10/15
- Số km
- 194
- Động cơ
- 239,261 Mã lực
- Tuổi
- 53
lớp 8 chưa sin cụ ơiĐề xuất của cụ làm lộ ra bài toán thuận mà bài toán này là bài toán nghịch.
E thử phát biểu bài toán thuận.
Cho hình thang cân BNEI có các góc đáy tại B, E = g = 20° và nhận BI, NE là phân giác; M là chân đường vuông góc hạ từ B xuống EI, BM cắt EI tại A. Cmr: h = BA/BN = 1.
Cm:
Ta có ^MNB = ^NBI + ^NIB= 3/2•g
-> ^MBN = 90° - 3/2•g = 90° - 30° = 60°.
Lớp 8: Vậy tam giác vuông MNB là 1/2 tam giác đều -> MB = 1/2BN
Mà AB = 2MB => h = AB/BN = 1 (dfcm)
Nhận xét: ở góc độ lớp 11 ta có: MB/BN = sin (^MNB) = sin (3/2•g)
-> h = AB/BN = 2•sin(3/2•g) (1)
Tức là với công thức (1) ta sẽ, biết g sẽ suy ra h (bài toán thuận), biết h sẽ suy ra g (bài toán nghịch type 1), biết h & g suy ra yếu tố còn lại (BE là phân giác góc NBI) (bài toán nghịch type 2)
Bài toán cụ thớt là bài toán ngược type 2 với h = 1 & g=20°.
Các cụ hoàn toàn có thể chế cháo thêm với g hoặc h bằng giá trị nào đó, để gen ra các bài toán thuận, nghịch khác.
- Biển số
- OF-389654
- Ngày cấp bằng
- 30/10/15
- Số km
- 194
- Động cơ
- 239,261 Mã lực
- Tuổi
- 53
cám ơn cụ !Góc AEB = 30 độ
Cách giải: lấy điểm H trên đoạn IB sao cho EH// AB => EH/AB= IE/IA=IE/IB (1).
Lấy điểm ạ trên IM sao cho Tam giác EHJ đều (J nằm trong phần của tam giác EHJ)
=>góc JEI = góc EIH = 20 độ (do tam giác EHJ đều nên góc HEJ = 60 độ và EH = EJ)
2 tam giác EIJ và IBE đồng dạng (trường hợp cạnh góc cạnh) do góc JEI= góc EIH = 20 độ
EJ/EI = EI/IB (do EJ=EH, EI=AB => EJ/EI =EH/AB= EI/IB (theo (1))
2 tam giác EIJ và IBE đồng dạng =>góc IBE = góc EIJ = 10 độ
=> góc ABE = góc ABI -EBI = 80-10 = 70 độ
=> góc AEB = 180-80-70 = 30 độ
- Biển số
- OF-389654
- Ngày cấp bằng
- 30/10/15
- Số km
- 194
- Động cơ
- 239,261 Mã lực
- Tuổi
- 53
cám ơn cụ !Lại mất tg rồi, hình như là 30 độ, dựng thêm hình tam giác đều là ra. Đây là tóm tắt lời giải

- Biển số
- OF-389654
- Ngày cấp bằng
- 30/10/15
- Số km
- 194
- Động cơ
- 239,261 Mã lực
- Tuổi
- 53
Bài này hơi khoai mợ à , bài trong đề học ainh giỏi quốc giaXấu hổ quá. Em đọc đầu bài 2 lần đều sai. Xin lỗi câc cụ
- Biển số
- OF-389654
- Ngày cấp bằng
- 30/10/15
- Số km
- 194
- Động cơ
- 239,261 Mã lực
- Tuổi
- 53
cụ siêu thế học hệ 10 năm mà giờ nhớ thế này là quá siêu , cách của cụ cũng hợp lý , để em tổng hợp các ý kiến rồi cho F1 tham khảo , bài này thuộc đề thi học sinh giỏi quốc gia nên hơi khó nhằnEm không làm được như cụ, hiểu phương pháp của cụ nhưng em chưa hiểu đoạn cuối cộng ra kết quả. Cho em sử dụng tri thức của cụ, modify 1 chút cho theo hiểu biết của em:
Trên IM lấy điểm N sao cho NB= AB (thay cho cụ lấy sao cho góc là 60 độ) -> tam giác ANB là tam giác đều (3 cạnh bằng nhau) và góc ABN = 60 độ.
góc NBI = ABI - ABN = (180-20)/2-60= 20.
Sau đó so tam giác BEI = INB (thay vì cụ so với IAN) theo kết quả so cạnh góc cạnh. Suy ra góc EBI = NIB = 10 độ -> góc BEI = 180-10-20 = 150 độ
Góc AEB = 180-BEI = 180-150 = 30 độ.
(P/S: E học hệ 10 năm, lớp 8 năm 74 chưa học món này)
Bài này kinh điển của hình học nâng cao lớp 8. Em nhớ đã gặp từ thời năm 1987, 1988. Để giải dc phải vẽ thêm tam giác đều như các Cụ đã làm ở trên.
Bọn luyện thi hsg đứa nào chả biếtBài này hơi khoai mợ à , bài trong đề học ainh giỏi quốc gia
The 80-80-20 Triangle Problem, Index to Solutions
- Biển số
- OF-787807
- Ngày cấp bằng
- 18/8/21
- Số km
- 337
- Động cơ
- 530,832 Mã lực
Bài hình HSG lớp 7. Thêm cho cụ một cách.
- Biển số
- OF-579316
- Ngày cấp bằng
- 15/7/18
- Số km
- 7,965
- Động cơ
- 1,084,926 Mã lực
E để cả 2 cách đó. Với hạn chế của lớp 8 thì chỉ xử được case đặc biệt là g=20°, h=1 thôi.
lớp 8 chưa sin cụ ơi
- Biển số
- OF-787807
- Ngày cấp bằng
- 18/8/21
- Số km
- 337
- Động cơ
- 530,832 Mã lực
Từ bài hsg lớp 7 nhưng thêm trục đối xứng lớp 8 nên thành bài lớp 8. Cách giải...nếu chỉ lớp 7 sẽ dài hơn.
- Biển số
- OF-431945
- Ngày cấp bằng
- 23/6/16
- Số km
- 12,392
- Động cơ
- 809,669 Mã lực
Lúc đó em mới nghĩ ra nên cách giải nó hơi loằng ngoằng, mục đích ban đầu em lấy góc 60 là để góc còn lại bằng 20 rồi dựa vào đó chứng minh 2 tam giác bằng nhau ở bước sau, đúng là nên lấy thẳng tam giác đều cho dễ hiểu thậtEm không làm được như cụ, hiểu phương pháp của cụ nhưng em chưa hiểu đoạn cuối cộng ra kết quả. Cho em sử dụng tri thức của cụ, modify 1 chút cho theo hiểu biết của em:
Trên IM lấy điểm N sao cho NB= AB (thay cho cụ lấy sao cho góc là 60 độ) -> tam giác ANB là tam giác đều (3 cạnh bằng nhau) và góc ABN = 60 độ.
góc NBI = ABI - ABN = (180-20)/2-60= 20.
Sau đó so tam giác BEI = INB (thay vì cụ so với IAN) theo kết quả so cạnh góc cạnh. Suy ra góc EBI = NIB = 10 độ -> góc BEI = 180-10-20 = 150 độ
Góc AEB = 180-BEI = 180-150 = 30 độ.
(P/S: E học hệ 10 năm, lớp 8 năm 74 chưa học món này)

Phần tính góc thì em dựa vào nguyên tắc tổng các góc trong một tam giác bằng 180 độ.
Như trong hình thì góc s + z = x + y + z = 180 độ, nên s = x + y, cái này hình như trong hình học có nói thì phải.
Thông tin thớt
Đang tải
Chia sẻ:
Bài viết mới
-
[HĐCĐ] Fadil với cung đường Đông Bắc 30/4/25
- Started by MinhDuc33
- Trả lời: 0
-
[Thảo luận] Xe Mazda 3 -2018 - Xỉa lái và Lệch Vô lăng khi chở đủ tải 5 người.
- Started by Nguyễn Quang Tín
- Trả lời: 0
-
-
-
-
[Funland] Đoàn Quân đội nhân dân Việt Nam tham gia Lễ duyệt binh trên Quảng trường Đỏ
- Started by Tien Tung
- Trả lời: 28
-
-
-
-
[Funland] Màn bắn súng thần công ở Huế bị lỗi kỹ thuật, pháo ‘lạc’ rơi vào khu vực du khách
- Started by lads1205
- Trả lời: 28

